






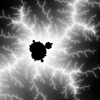

































The Mandelbrot Set is a set named after Benoit Mandelbrot who first obtained high-quality visualizations of the set in 1980. While not technically a fractal, it contains within itself many similar copies of the entire set. Zooming in at the boundary of the set (in black) reveals hidden treasures. See Mandelbrot Set








































